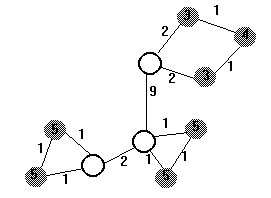
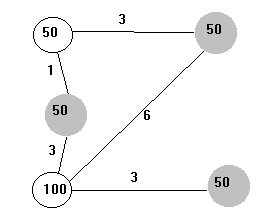
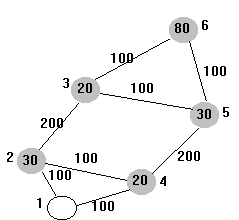
Téma A: Optimálny evakuačný plán
Vypracujte co nejlevnější evakuační plán obcí ze seznamu J, kde každá obec j má bj obyvatel, vozidly z tří různých homogenních autoparků umístěných v místech A, B, C. V místě A je umístěn autopark složený z vozidel, kde každé má kapacitu 70 osob, denní amortizační náklady vozidla jsou 2000 Sk a náklady na jeden kilometr jízdy jsou 30 Sk. V místě B je umístěn autopark složený z vozidel, kde každé má kapacitu 40 osob, denní amortizační náklady vozidla jsou 1400 Sk a náklady na jeden kilometr jízdy jsou 20 Sk. V místě C je umístěn autopark složený z vozidel, kde každé má kapacitu 50 osob, denní amortizační náklady vozidla jsou 1500 Sk a náklady na jeden kilometr jízdy jsou 25 Sk. Při evakuaci, která má proběhnout jednorázově, může být každé vozidlo použito jen jednou a předpokládá se, že vyjede na místo určení a vrátí se s evakuovanými osobami do svého autoparku. V daný den nebude vozidlo použito k jiným účelům a v místě C je k dispozici nejvýše 100 vozidel.
Vaší úlohou je
- pro zadaná místa A, B, C a množinu obcí J a pro zadané parametry, vypočítat optimální přidělení vozidel obcím,
- vyšetřit citlivost získaného řešení na změnu jednotkových nákladů na jeden km jízdy v intervalu <10,60> Sk pro vozidla umístěná v A,
- znázornit výsledek úlohy z 1) graficky na mapě a provést kontrolu přípustnosti optimálního řešení z 1).
Doporučené cvičenia k jednotlivým odprednášaným témam
(Odkazy na čísla stránok sa vzťahujú na skriptá Janáček, J.: Operační analýza 1)
Téma 1 a 2 :
úloha plánování výroby, cvičení na straně 19,
úloha s výrobním receptem, cvičení na straně 20,
řezná úloha, cvičení na straně 22,
směšovací úloha, cvičení na straně 24,
dopravní úloha, cvičení na straně 27,
násobná dopravní úloha, cvičení na straně 32,
dopravní úloha se ztrátami, cvičení na straně 34,
minimaxová dopravní úloha, cvičení na straně 35,
úloha o maximálním toku, cvičení na straně 39,
úloha o nejlevnějším toku, cvičení na straně 41,
úloha o obnovitelných součástkách, cvičení na straně 46,
úloha o návrhu logistického systému, cvičení na straně 49.
Téma 3 :
cvičení na geometrická místa bodů, strana 57,
cvičení na zobrazování množiny přípustných řešení, strana 60,
cvičení na geometrickou optimalizaci, strana 62,
cvičení na konvexnost, strana 63,
cvičení na konvexní kombinaci, strana 64,
cvičení na konvexní polyédr, strana 65.
Téma 4 :
cvičení na existenční větu lineárního programování, strana 67,
cvičení na bazické přípustné řešení, strana 71.
Téma 5 :cvičení na simplexovou metodu, strana 81, 83, 84, 93.
Téma 6 :>cvičení na vztah mezi tabulkami simplexové metody, strana 105.
Téma 7 :
cvičení na citlivost optimálního řešení na změny koeficientů účelové funkce, strana 120,
cvičení na citlivost optimálního řešení na změny pravé strany soustavy, strana 124,
cvičení na parametrické programování, strana 128,, 130, 132.
Téma 9 :
přiřazovací úloha, cvičení na straně 139,
převod úloh CLP na 0-1 programování, cvičení na straně 140,
alokační (rajonizační) úloha, cvičení na straně 143,
úloha o rozmístění dopravní flotily, cvičení na straně 147,
úloha přidělování dopravních prostředků, cvičení na straně 149,
dopravní úloha s kontejnery, cvičení na straně 150,
dopravní úloha s fixní sazbou, cvičení na straně 153,
lokační (umisťovací)úloha, cvičení na straně 156,
úloha o umisťování škodlivých zařízení, cvičení na straně 157,
úloha o nejkratší cestě, cvičení na straně 160,
úloha obchodního cestujícího, cvičení na straně 163,
úloha okružních jízd, cvičení na straně 164, 165,
úloha o rozkladu množiny, cvičení na straně 166,
modelování logických podmínek, cvičení na straně 167.
Další cvičení je možno nalézt v "příkladech na rozmyšlení".
 J a jí nejbližším střediskem (úloha o p-centrech).
Vaší úlohou je
J a jí nejbližším střediskem (úloha o p-centrech).
Vaší úlohou je
 J a jí nejbližším střediskem (úloha o p-centrech).
Vaší úlohou je
J a jí nejbližším střediskem (úloha o p-centrech).
Vaší úlohou je
 J. Vybudování meziskladu stojí v přepočtu na plánovací období 100000 Sk. Je třeba zjistit, zda mají být budované mezisklady, pokud ano, tak kolik a v kterých obcích.
J. Vybudování meziskladu stojí v přepočtu na plánovací období 100000 Sk. Je třeba zjistit, zda mají být budované mezisklady, pokud ano, tak kolik a v kterých obcích.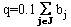 .
.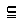 En je konvexná množina. Dokážte, že množina Q={y/y=ß.x, x
En je konvexná množina. Dokážte, že množina Q={y/y=ß.x, x K} je tiež konvexná. Pozn. Q získate tak, že každý prvok množiny K vynásobíte reálnym číslom ß.
K} je tiež konvexná. Pozn. Q získate tak, že každý prvok množiny K vynásobíte reálnym číslom ß.
 K, y
K, y  Q}. Rozhodnite, či Minkovského súčet dvoch konvexných množín z En je alebo nie je konvexná množina. Dokážte!
Q}. Rozhodnite, či Minkovského súčet dvoch konvexných množín z En je alebo nie je konvexná množina. Dokážte!
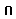 , - (zjednotenie, prienik, rozdiel dvoch množín) rozhodnite, či a za akých okolností je pre konvexné množiny Q a K výsledok operácií Q U K, Q
, - (zjednotenie, prienik, rozdiel dvoch množín) rozhodnite, či a za akých okolností je pre konvexné množiny Q a K výsledok operácií Q U K, Q 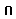 K, Q-K konvexná.
K, Q-K konvexná.
 1, |x2|
1, |x2|  1, |x3|
1, |x3|  1
1
 1
1
 x1
x1  x2
x2  x3
x3
 1
1
 1, |x1|
1, |x1|  2, |x2|
2, |x2|  2, |x3|
2, |x3|  2
2
 |x2|
|x2|  |x3|
|x3|
 |x2|
|x2|  |x3|
|x3|  1
1
 1, x1
1, x1 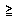 0, x2
0, x2 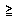 0, x3
0, x3 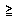 0
0
 x1
x1  x2
x2  x3 ako nezápornú kombináciu troch bodov.
x3 ako nezápornú kombináciu troch bodov.
6 (2) 3x1 + 2x2
16 (3) xj
0 pre j=1..4
 < 0,
< 0, 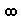 >.
>.
 E2} z počatočného bodu x = <3, 3>T s prestnosťou
E2} z počatočného bodu x = <3, 3>T s prestnosťou  = 0.1
= 0.1 E2} z počatočného bodu x = <2, 2>T s prestnosťou
E2} z počatočného bodu x = <2, 2>T s prestnosťou  = 0.1
= 0.1 E2, (x1-2)2 + (x2 - 3 )2 <= 1} Z POČIATOČNÉHO BODU
X = <2, 3>T metódou pokutových funkcií.
E2, (x1-2)2 + (x2 - 3 )2 <= 1} Z POČIATOČNÉHO BODU
X = <2, 3>T metódou pokutových funkcií.
 E2 : x1
E2 : x1  <-1,3> }
<-1,3> }
 E2 : x1 - x2 <=1,
X1 - x2 >= -1}
E2 : x1 - x2 <=1,
X1 - x2 >= -1}
 E2 : x12 + x22 <=1, (X1 - 1)2 +
x22 <= 1}
E2 : x12 + x22 <=1, (X1 - 1)2 +
x22 <= 1}
 E2 : x1 >= 0,
x2>= 0, x1 + x2 <= 2}
E2 : x1 >= 0,
x2>= 0, x1 + x2 <= 2}
 E2 : x patrí do konvexného obalu <1, 1>, <2, 1>, <1, 2>}
E2 : x patrí do konvexného obalu <1, 1>, <2, 1>, <1, 2>}
 E2 : x1
E2 : x1  <-1, 1>, x2
<-1, 1>, x2  <0, 2>}
<0, 2>}
 <-4, 3>tak, aby obrázok bol čo najväčší a pritom aby na obrazovke boli obe krivky celé. Určte optimálny zobrazovací rozsah na zvislej osi.
<-4, 3>tak, aby obrázok bol čo najväčší a pritom aby na obrazovke boli obe krivky celé. Určte optimálny zobrazovací rozsah na zvislej osi.
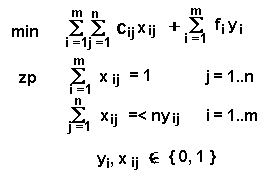
 { 0, 1}podmienkami nezápornosti a tam, kde je potrebné yi<=1 A ZOSTAVTE DUÁLNU ÚLOHU. ( ČO INTERPRETÁCIA DUÁLNYCH PREMENNÝCH ?)
{ 0, 1}podmienkami nezápornosti a tam, kde je potrebné yi<=1 A ZOSTAVTE DUÁLNU ÚLOHU. ( ČO INTERPRETÁCIA DUÁLNYCH PREMENNÝCH ?)
 a v grafe
a v grafe  .
.